Overview Under the direction of Professor John Hubbard, I have developed two graphics programs that draw surfaces in three dimensions. The first program draws two-dimensional manifolds defined by implicit equations. The second program draws stable and unstable two-dimensional manifolds defined by differential equations. Both programs can be used to study any equation of the appropriate type without additional programming. Also, both programs allow the user to rotate surfaces on-screen in real time. I am planning to apply the second program to studying the Lorenz equations. The first program: Manifold The first program draws surfaces that can be represented by equations of the form 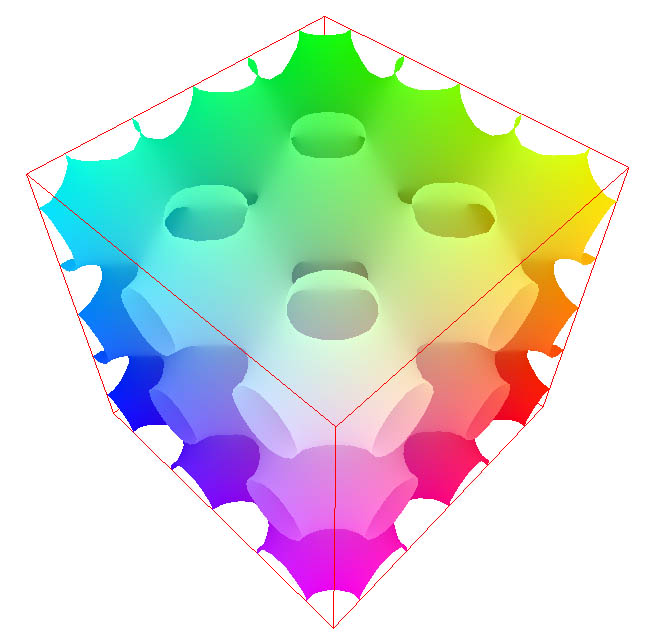0=f(x,y,z). This is a general implicit form for surfaces. The program does not require the surface to be parameterized. The surface above is represented by the equation 0=x^2+y^2-z^2-1/4. The surface to the right is represented by the equation 0=sin(x)+sin(y)+sin(z). How does it work? The program first divides into a large number of small cubes the region of space in which the surface will be drawn. The program next analyzes each cube and constructs the surface interior to the cube. Finally, the program coordinates the surfaces in adjacent cubes to construct the full geometry of the surface. The location of each point of the surface determines the color of the point. The Second Program Written and designed by Adam Barth. February 17, 2000